Estabilidad de Taludes. Suelos

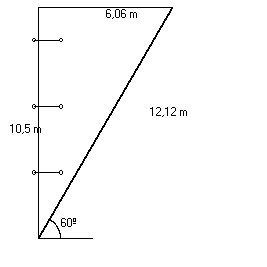
En un talud de una carretera se han producido una serie de inestabilidad que en principio se deben a fenómenos de deslizamiento activos en la zona.

El talud, asimilable a un suelo arcilloso presenta las siguientes características geotécnicas:
c (cohesión) = 65 kN/m²
φ (áng rozamineto) = 18º
γ (peso específico) = 19,2 kN/m³

El talud presenta una altura máxima de 24 m, y se estima una sobrecarga de 0,5 T/m² en el mismo. El ángulo de talud en la zona es de 65º.

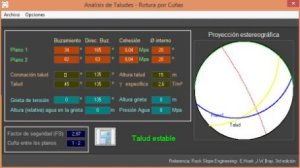
Para calcular la estabilidad del talud, recurrimos a los ábacos de Taylor. Concretamente los cálculos los hacemos con un programa informático. Se introducen los datos tal cual, a excepción de la altura del talud, en la que además consideramos la sobrecarga (sobrecarga / peso específico).

Obtenemos un FS = 1,2; que indica que el talud es inestable y por tanto la existencia de deslizamientos queda demostrada y justificada.

Para corregir el talud, y aumentar el FS a valores estables (1,5) existirían varios métodos, todos ellos condicionados económicamente.

La solución mas rápida desde el punto de vista teórico es reducir el ángulo del talud, adoptando un ángulo de 55º, obtenemos un FS = 1,5.

Sin embargo, es una solución totalmente inviable desde el punto de vista económico y técnico. Teniendo en cuenta que dicha modificación afectaría a un tramo aproximado de 800m, y que el volumen de tierra es de aproximadamente 750 m³ por metro lineal, supondría un volumen de tierra inadmisible.

Utilizando el mismo ábaco de Taylor (o dicho de otra manera, el mismo programa), podemos calcular la altura crítica para un FS dado. En este caso, insertando el FS deseado, obtenemos un altura crítica de 19,5 m.

Es decir, nos sobran 5m de altura de talud para considerarlo estable. La solución ahora, ya no se centra en el talud, sino en estabilizar esos 5 m de talud, por lo que se puede optar por crear una berma de seguridad y reducir el ángulo del talud para esos metros, o adoptar soluciones mas drásticas, efectivas y sobretodo duraderas, como es el caso de recurrir a micropilotes o pilotes, creando una pantalla que reduzca el círculo de deslizamiento para el talud. En este último caso, adoptando una pantalla de micropilotes a de 15m, nos quedan 13m de talud con posibilidad de ser inestable, sin embargo, un simple cálculo nos ofrece un valor de FS = 2,91 y por tanto estable.

Cálculo de la tensión de anclaje en macizos rocosos

Uno de los métodos mas sencillos y fiables es el propuesto por Kovari y Fritz en 1976 para roturas planares.

Los datos de partida se obtienen del estudio geotécnico y de la observación geométrica del macizo rocoso.

Una vez establecidos los datos geométricos de la superficie de deslizamiento, se puede calcular matemáticamente el volumen de la masa de roca que puede entrar en movimiento.

Los datos esenciales para el cálculo son:
– longitud del plano de deslizamiento
– ángulo superficie terreno respecto a la horizontal
– ángulo superficie de deslizamiento respecto a la horizontal

Las propiedades geotecnicas del macizo rocoso a conocer son:
– cohesión en la superficie de deslizamiento
– ángulo de rozamiento interno de la superficie de deslizamiento
– densidad (peso específico)

El método de cálculo permite establecer un esfuerzo de anclaje para un determinado coeficiente de seguridad.

Asimismo, y en base a la experiencia del técnico competente, ese esfuerzo de anclaje se puede repartir en varias filas a lo alto de la superficie del muro, reduciéndose así la tensión por anclaje.

Como recomendación final, en muros de cierta altura (>10m) y con macizos rocosos homogéneos se suele elegir una fila de anclajes cada 2,5 m de altura.

Ejemplo:

Coeficiente de seguridad a considerar: 1,5
Peso del macizo rocoso que puede deslizar (T/m) 76,4
Longitud del plano de deslizamiento (m) 12,12
Cohesión en la superficie de deslizamiento (T/m²) 5
Angulo de anclaje con el plano horizontal (º) 15
Angulo del plano de deslizamiento con el plano horizontal (º) 60
Angulo de rozamiento de la superficie de deslizamiento (º) 22

Esfuerzo de anclaje total calculado (T/m):29,81

Muro tipo recomendado:
Altura del muro.: 10,5 m
Separación en la vertical.: 2,5 m
Nº de filas anclajes (cada 2,5 m de altura).: 4
Tensión por anclaje.:18,63 T

Muro tipo calculado según criterio técnico:
Número de filas.:3
Separación entre anclajes.: 3 m
Tensión por anclaje.: 29,81 T

Datos de la masa de roca a deslizar:
Angulo superficie de deslizamiento con la horizontal.: 60º
Angulo superficie terreno – horizontal.: 0º
Volumen.: 31,82 m³
Densidad.: 2,40 T/m³

Empujes sobre un muro. Empuje activo

Uno de los apartados del estudio geotécnico, es el referido a los empujes en caso de haber sótanos, contención de tierras, …

En el siguiente ejemplo, se realiza un estudio geotécnico para la caracterización geotécnica de un terreno que se va a excavar y que para su contención se va a construir un muro en ménsula.

En este caso, contamos con un nivel freático y el trasdós del muro no es vertical, siendo el ancho de coronación del muro menor que la base. Los datos geométricos del muro no son de importancia ya que no se va a calcular ni dimensionar el muro.

Los datos de partida son:
ángulo de rozamiento terreno  φ = 25º
ángulo de rozamiento muro – terreno  δ = 15º (según CTE)
ángulo terreno coronación  β = 15º
peso específico suelo seco  γ = 23 kN/m³
peso específico suelo sumergido γ’= 13 kN/m³
peso específico agua γw = 10 kN/m³
ángulo trasdos – horizontal = 86,6º (por geometría)
altura del muro (desde la base de cimentación) H = 3,0 m
altura del nivel de agua desde coronación muro h = 1,6 m

Para calcular el coeficiente de empuje activo, se utilizan las fórmulas clásicas que se pueden consultar en cualquier bibliografía. En nuestro caso, estamos en el peor de los casos posibles a efectos de cálculo, trasdós no vertical, presencia de agua, …

Obteniendo:
coeficiente de empuje activo   Ea = 0,504
coeficiente de empuje activo horizontal  Eah = 0,478
coeficiente de empuje activo vertical    Eav= 0,159

Para calcular el empuje activo, y dado que tenemos nivel freático, se descompone este empuje en los siguientes:
– empuje debido al nivel de tierras por encima de la capa freática
– empuje debido a la carga equivalente del nivel superior sobre el nivel sumergido
– empuje debido al nivel de tierras sumergido
– empuje debido al nivel del agua en la zona sumergida

a) Empuje debido al nivel de tierras por encima de la capa freática

Siendo z la altura del nivel del terreno situado por encima del nivel de agua y y el peso específico del terreno seco.
El valor obtenido para el empuje = 14,84 kN/m
En cuanto a la presión del terreno:

Siendo P = 18,55 kN/m²
Y el punto de aplicación de este empuje se puede calcular mediante y=2z/3 = 1,07m

b) Empuje debido a la carga equivalente del nivel superior sobre el nivel sumergido

Siendo H la altura total de muro desde la base de cimentación.
El valor obtenido para el empuje = 25,97 kN/m
y la presion del terreno P = 18,55 kN/m²
En este caso, el punto de aplicación es y=z+(H-z)/2 = 2,30 m.

c) Empuje debido al nivel de tierras sumergido

Utilizando en este caso el valor del peso específco del suelo sumergido. El valor de E = 6,42 kN/m.
La presión P = 9,17 kN/m²
El punto de aplicación se calcula mediante y= z + 2(H-z)/3 = 2,53 m

d) Empuje debido al nivel del agua en la zona sumergida

E = 9,8 kN/m
La presión P = 14,0 kN/m²
El punto de aplicación se calcula mediante y= z + 2(H-z)/3 = 2,53 m

Con estos valores, se puede calcular el valor de la componente horizontal y vertical del empuje activo sobre el muro.

Obteniendo:
Empuje activo horizontal = 54,60 kN/m
Empuje activo vertical = 15,49 kN/m
Y el punto de aplicación de la resultante del empuje activo:

y = 2,05 m

Estabilidad de Taludes. Rotura por cuñas.

Se plantea la realización de un talud de 15 m de altura adoptando un ángulo de 45º. El macizo rocoso, está formado por una alternancia de calizas y margocalizas dispuestas en estratos centimétricos (15-50cm). Los parámetros geotécnicos, obtenidos a partir de una estación geomécanica realizada in situ han sido los siguientes: c = 40 kN/m², ángulo de rozamiento interno 20º.

El talud, tendrá una dirección N040ºE y un buzamiento al SE. Se han detectado y medido las siguientes familias de discontinuidad:

E = 165/34º; J1 = 355/60º; J2 = 063/82º

De la proyección estereográfica se deduce una posible rotura por cuñas a favor de E-J1 y otra a favor de E-J2.

Para calcular la estabilidad de la posible rotura, se sigue la metodología empleada por Hoek y Bray (1977) descrita en el Manual de Taludes (IGME).

En un primer lugar, se adopta el método rápido considerando que si el factor de seguridad para terreno seco y sin cohesión es mayor de 2,0, se puede afirmar que el talud será estable en las peores condiciones de presión intersticial.

(A y B se obtienen de los ábacos para rotura por cuñas correspondientes). Obteniéndose:
E-J1        FS = 3,60
E-J2        FS = 0,61

La primera cuña, por tanto será estable, en el caso de la segunda se debe recurrir a una metodología mas precisa, en la que se tendrá en cuenta todos los factores que intervienen en la estabilidad del talud (altura, presencia de agua, parámetros geotécnicos, buzamientos, …). En este segundo caso, se debe volver a recurrir a las proyecciones estereográficas para el cálculo de los ángulos entre planos.


Siendo:

X= 5,68; Y=2,45; A=1,47; B=5,47

obteniéndose un valor de FS = 2,487 y siendo por tanto estable.

En la actualidad existen muchos programas informáticos que simplifican estos cálculos, aunque sus resultados dependen de la experiencia y criterio del técnico que introduce los datos.

Existen aplicaciones sencillas, que calculan el FS a partir de los datos obtenidos en la proyección estereográfica:

Y los que a partir de los datos geoestructurales medidos en campo y con los parámetros geotécnicos obtenidos en la estación geomecánica, calculan el FS.

Muros de Escollera

En el siguiente ejemplo, calcularemos un muro de escollera de 4,00 m de altura máxima. La función de este muro es la de estabilizar un talud natural.

Para el correcto dimensionado, cálculo y comprobación de este tipo de muros, hay que recurrir a la siguiente bibliografía:

– Guía para el proyecto y ejecución de muros de escollera en obras de carretera (2006)

– Recomendaciones para el diseño y construcción de muros de escollera en obras de carreteras, del Ministerio de Fomento (1998).

Geometría de la sección tipo del muro:

Entre el muro y el trasdós se instalará una capa de de aproximadamente 1m de espesor, de material granular.

Un aspecto importante a destacar en este tipo de muros, es la cimentación del mismo. Se requiere de un estudio geotécnico previo que establezca y defina adecuadamente tanto los parámetros geotécnicos del terreno a «sujetar»  como el nivel de cimentación adecuado y sus propiedades resistentes.

En nuestro ejemplo, especularemos con una cimentación en un nivel rocoso con una presión admisible de 0,5 Mpa (5 kg/cm²).

Siguiendo las recomendaciones para el diseño y construcción de muros de escollera en obras de carreteras, se obtiene la situación problema. En nuestro caso, sería una situación IIs.

Los valores que usaremos serán:

Hormigón de la cimentación: en masa; HM-20.
– material del trasdós:
ángulo de rozamiento interno: 25º
peso específico: 1900 kg/m³
sobrecarga estimada en trasdós: 3 T/ml (según normas)
– escollera de árido calizo de cantera.
tg E = 2
peso específico = 1900 kg/m³
ancho en coronación (del ábaco IIs) a = 1,50 m
ancho del muro en la base (b= a+H/10) = 1,90 m
Con estos datos básicos, se puede definir la geometría total de la escollera, para posteriormente calcular su estabilidad a deslizamiento y vuelco. Generalmente las escolleras se utilizan como métodos de contención de suelos, por lo que además, habría que realizar cálculos de estabilidad global basándonos en la hipótesis de deslizamiento circular de suelos.

Comprobación de la escollera:

Partiendo de los siguientes datos, podemos obtener el resto de valores del gráfico:

a (ancho coronación) = 1,5 m
b (ancho en la base) = 1,9 m
x0 (puntera) = 0,3 m
altura z (cimentación) = 0,714 m + 1 m (según norma)
altura total escollera = 5,714 m
ancho total en la base = 2,2 m
trasdós (º) = 78,69
intradós (º) = 73,30

y con la geometría definida, obtenemos:
peso total del muro de escollera = 18,0 T
volumen escollera = 10,25 m³
volumen excavación cimientos = 3,24 m³
volumen relleno granular = 5,81 m³

Del estudio geotécnico obtenemos:
peso específico terreno: 1,9 T/m³
ángulo rozamiento terreno: 20º
ángulo rozamiento escollera-terreno = 13,33º
ángulo rozamiento cimiento (zapata-terreno) = 35º

Con las fórmulas clásicas, obtenemos el valor de los empujes y fuerzas resultantes
Ka (coeficiente empuje activo) = 0,525
empuje activo debido al terreno = 16,28
empuje debido a la sobrecarga = 8,99
Empuje Activo (Ea) = 25,28
Fuerzas estabilizadoras = 24,07 T/m²
Fuerzas desestabilizadoras = 12,76 T/m²
Momento estabilizador = 27,98 mTm
Momento volcador = 13,04 mTm

Y a partir de las fuerzas y momentos estabilizadores y desestabilizadores, obtenemos el coeficiente de estabilidad al vuelco y el coeficiente de estabilidad al deslizamiento.

Coeficiente estabilidad vuelco = 2,14 (ESTABLE)
Coeficiente estabilidad deslizamiento = 1,89 (ESTABLE)

Sobre la seguridad al hundimiento, la escollera presenta un axil de 0,95 kg/cm² (0,01 Mpa) siendo la presión admisible del terreno de 5 kg/cm² (0,5 Mpa), por lo que cumple, y no habrá problemas de hundimiento.

En cuanto a la estabilidad global, lo ideal es considerar el muro de escollera como una capa de suelo, estableciendo la geometría del mismo y adoptando unos valores geotécnicos de 20 kN/m³ de densidad (en caso de bloques calizos), para el ángulo de rozamiento entre 50-60º y una cohesión de 0, analizando el problema como si fuera un suelo con rotura circular.

Se debe tener en cuenta que el punto mas desfavorable en este tipo de muros es su nivel de apoyo o empotramiento, por lo que las superficies de rotura a considerar serán aquellas que pasan bajo su base, adoptando un factor de seguridad no inferior a 1,5.