Cimentaciones. Rellenos mejorados

En ocasiones, dada las características del terreno no queda otra que realizar una cimentación de tipo superficial sobre una zona rellenada previamente (por ejemplo terrenos ganados al mar).

En este tipo de situaciones es muy importante conocer tanto las cargas transmitidas al terreno como la naturaleza del relleno y su puesta en obra, siempre teniendo en cuenta los problemas de subsidencias y colapsos que sufren este tipo de terrenos, para ello es fundamental una campaña de exploración geotécnica precisa y como se ha apuntado anteriormente, conocer como ha sido la puesta en obra de los materiales de relleno (compactación, tipología, …).

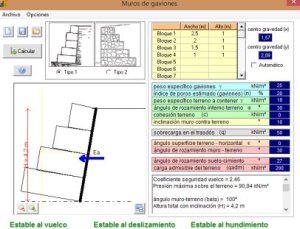
En nuestro ejemplo, se nos presenta el caso de un pabellón industrial, que transmitirá un carga máxima al terreno de 75 kN/m². La zona de relleno se ha realizado sin control geotécnico, con material heterogéneo compuesto por bloques pétreos (volúmenes de hasta m³) y arcillas. La zona se ha sométido a intensas pasadas con apisonadoras y a priori el conjunto se encuentra bien compactado, al menos en los primeros metros.

La exploración geotécnica ha consistido en calicatas y penetrómetros, y tal cual está el terreno, se descarta cualquier tipo de cimentación sobre el terreno.

Por lo tanto, lo idóneo (por motivos económicos queda totalmente descartada cualquier tipo de cimentación profunda) es realizar un relleno mejorado sobre el relleno existente.

Para ello, en necesario preparar una base adecuada para las zapatas (corridas en este caso) garantizando un apoyo uniforme y evite que la cimentación sufra heterogeneidades en este plano de apoyo.

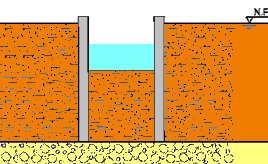
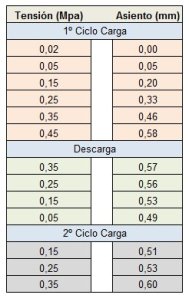
Se recomienda realizar una excavación de aproximadamente 2,00 m (zona sobreconsolidada) con una anchura mínima en función del ancho de la zapata. El fondo de esta excavación deberá ser alisado con un rodillo de peso estático y dando sucesivas pasadas (mínimo 4). Esta excavación se rellenará con material de características geotécnicas conocidas y deberá ser compactado con el rodillo de peso estático hasta alcanzar un nivel de compactación adecuado (comprobable mediante ensayo proctor y/o densímetro nuclear).

Para «sellar» este relleno mejorado, se deberá verter una capa de hormigón de unos 5 cm de espesor, sobre la cual se realizará la zapata.

De esta manera, el relleno mejorado absorberá las cargas transmitidas y a su base se transmitirán 10 kN/m², presiones de trabajo mínimas y sobradamente soportables por el relleno existente.

Muros de contención. Gaviones

En el siguiente ejemplo, se calculará la estabilidad de un muro de contención de gaviones.

Las características del muro son las de la figura:

Los bloques de gaviones estarán constituidos por bloques calizos de peso específico 25 kN/m³ y un índice de poros estimado del 20%. Los bloques están soldados unos a otros en la fila, constituyendo a efectos de cálculo un único bloque.

Este muro se encuentra sobre una base de hormigón pobre, presentando el terreno sobre su base una capacidad portante de 150 kN/m². La inclinación respecto la vertical es de 10º, siendo la altura por bloque de 1 m (total 4m).

El terreno a contener tiene las siguientes carcaterísticas:
peso específico = 18,5 kN/m³
cohesión = (no se tiene en cuenta a efectos de cálculo)
ángulo de rozamiento = 30º
sobrecarga = 50 kN/m²
ángulo superficie – horizontal = 0º

---

En primer lugar, se calculará la altura total del muro dado que presenta una inclinación hacia el terreno.
H = [h+ (B-a) tg α] cos α) = 4,2 m.
La sobrecarga sobre el terreno, se aplicará en los cálculos como una altura equivalente, h1 = q/y= 2,7 m.
El volumen (V) y masa de los gaviones será: 7 m³ y 140 kN
Ángulo total entre el muro y la masa de tierra a contener = 100º

Con las fórmulas clásicas de empujes, calculamos el coeficiente de empuje activo y el valor de dicho empuje.

Siendo:
Ka = 0,227
Ea = 84,66 kN/ml
Del mismo modo, se calcula la profundidad de aplicación tanto de la componente horizontal como de la vertical de dicho empuje.
Hv1 (vertical) = 1,36 m
Hh1 (horizontal) = 2,78 m
Y a continuación, los valores de empuje activo vertical y horizontal.
Eah = 79,5 kN/ml
Eav = 28,9 kN/ml

Seguridad al deslizamiento

n = 1,55 > 1,5 y por tanto, estable al deslizamiento

Seguridad frente al vuelco

Debemos conocer el centro de gravedad del muro, que se obtiene fácilmente del dibujo o bien por trigonometría.
x = 1,35 m; y = 2,11 m
El momento volcador (Mv) será el Eav * profundidad de aplicación; Mv = 108,19 mKN
El momento resistente (Mr) será Eah * s’ + Eav * s; siendo s el punto de aplicación del Eav y s’ obtenido geométricamente a partir de x e y. s’ = 1,7; Mr = 318,5 mKN

Resultado = 318,5 / 109,19 = 2,95 > 1,5 y por tanto estable al vuelco

Seguridad frente al hundimiento

Si e < B/6 quiere decir que la resultante cae dentro del núcleo central y las tensiones se pueden calcular con la fórmula:
σ = N/B + (1 + 6e /B)

Siendo:
N = 180,20 kN/m
e = 0,08 < 0,42 m
σ = 85,92 kN/m²

Siendo σ < qadm del terreno, y por tanto estable.

Estabilidad de Taludes. Suelos

En un talud de una carretera se han producido una serie de inestabilidad que en principio se deben a fenómenos de deslizamiento activos en la zona.

El talud, asimilable a un suelo arcilloso presenta las siguientes características geotécnicas:
c (cohesión) = 65 kN/m²
φ (áng rozamineto) = 18º
γ (peso específico) = 19,2 kN/m³

El talud presenta una altura máxima de 24 m, y se estima una sobrecarga de 0,5 T/m² en el mismo. El ángulo de talud en la zona es de 65º.

Para calcular la estabilidad del talud, recurrimos a los ábacos de Taylor. Concretamente los cálculos los hacemos con un programa informático. Se introducen los datos tal cual, a excepción de la altura del talud, en la que además consideramos la sobrecarga (sobrecarga / peso específico).

Obtenemos un FS = 1,2; que indica que el talud es inestable y por tanto la existencia de deslizamientos queda demostrada y justificada.

Para corregir el talud, y aumentar el FS a valores estables (1,5) existirían varios métodos, todos ellos condicionados económicamente.

La solución mas rápida desde el punto de vista teórico es reducir el ángulo del talud, adoptando un ángulo de 55º, obtenemos un FS = 1,5.

Sin embargo, es una solución totalmente inviable desde el punto de vista económico y técnico. Teniendo en cuenta que dicha modificación afectaría a un tramo aproximado de 800m, y que el volumen de tierra es de aproximadamente 750 m³ por metro lineal, supondría un volumen de tierra inadmisible.

Utilizando el mismo ábaco de Taylor (o dicho de otra manera, el mismo programa), podemos calcular la altura crítica para un FS dado. En este caso, insertando el FS deseado, obtenemos un altura crítica de 19,5 m.

Es decir, nos sobran 5m de altura de talud para considerarlo estable. La solución ahora, ya no se centra en el talud, sino en estabilizar esos 5 m de talud, por lo que se puede optar por crear una berma de seguridad y reducir el ángulo del talud para esos metros, o adoptar soluciones mas drásticas, efectivas y sobretodo duraderas, como es el caso de recurrir a micropilotes o pilotes, creando una pantalla que reduzca el círculo de deslizamiento para el talud. En este último caso, adoptando una pantalla de micropilotes a de 15m, nos quedan 13m de talud con posibilidad de ser inestable, sin embargo, un simple cálculo nos ofrece un valor de FS = 2,91 y por tanto estable.

Sifonamientos. Tablestacas

En general, se va a producir un levantamiento del fondo de la excavación cuando se anulen las tensiones efectivas y existir unas fuerzas de infiltración «hacia arriba».

En el siguiente ejemplo, tenemos un terreno limoso (ML según SUCS) sobre un nivel aluvial de gravas y arenas de varias decenas de metros.

En el momento de inicio de la excavación el nivel freático estará en superficie; en varios sondeos realizados en la zona, ha sido surgente. Por lo que se recomienda un bombeo constante durante la excavación y realizarla al abrigo de tablestacas.

Datos:
γsat = 18 kN/m³, cu = 1,3 T/m²
espesor del nivel = 6 m
permeabilidad = 0,000045 m/s
profundidad de la excavación = 4 m

Para evitar el sifonamiento, no se debe llegar al gradiente hidraúlico crítico (Ic).
Ic = (γsat / γw) – 1 = 0,80

Mediante la expresión (Ic * espesor nivel) / (Ic +1) obtenemos la profunidad a la que se alcanza el gradiente crítico; profundidad por debajo de la cúal se producirá sifonamiento, y que en este caso es de 2,67 m, y dado que nuestra excavación será de 4 m tendremos problemas de sifonamiento.

Como se indicó al principio, la excavación se realizará al abrigo de tablestacas, siendo su alcance limitado por el valor de rechazo del SPT obtenido en el nivel aluvial de gravas a una profundidad de 9,5 m. La longitud de la tablestaca será de 8 m (6m nivel de limos + 2 m en gravas).

El gradiente medio en la pantalla de tablestacas, se puede obtener mediante i = AH/L. Siendo AH la diferencia de potencial entre 2 puntos (diferencia entre n.f. y base de la excavación) y L distancia en la dirección de flujo entre estos dos puntos. Siendo i = 0,4.

El factor de seguridad, una vez conocidos tanto i como ic será; FS=ic / i = 2, superior a 1,5 y por tanto, con esta longitud y empotramiento de las tablestacas, no se producirá sifonamiento.

Al tiempo, se nos exige un cálculo justificativo para las necesidades de bombeo. Éste, se puede calcular mediante la fórmula: Q = k · H · (Hp / Lp), siendo:

Q = caudal que se filtra por debajo de la pantalla
K = permeabilidad (0,000045 m/s)
H = diferencia entre la posición del nivel freático y la base de la tablestaca
Hp = profundidad de la tablestaca bajo la base
Lp = longitud total de la pantalla

Siendo el caudal esperado Q = 0,000021 m/s, que aunque se considera medio-bajo (según tablas) requerirá de un bombeo continuo.

Corrección ensayo SPT. UNE EN ISO 22476-3:2006

El valor obtenido del ensayo SPT en un sondeo índica el valor N30, sin embargo, en diversos cálculos se requiere el valor corregido para una energía del 60%.

La norma UNE EN ISO 22476-3:2006 establece los criterios para obtener los factores de corrección para cualquier energía.

Sin embargo, tal como índica la propia norma, para el cálculo del valor SPT corregido, tan solo se deberían aplicar aquellos específicos para cada caso en concreto.

El ensayo SPT consiste en introducir mediante hinca un tomamuestras normalizado en el terreno. Es un ensayo que se ejecuta en sondeos y consiste básicamente en dejar caer una maza de 63,5 kg desde una altura de 76 cm contando el número de golpes necesarios para introducir el tomamuestras 60 cm en el terreno (4 tramos de 15 cm), siendo el valor N30 el correspondiente al golpeo del tramo central de 30 cm.

Existen varios tomamuestras, con el de «cuchara», se puede obtener una muestra que dependiendo del tipo de suelo y ejecución se puede considerar inalterada.

Energía teórica del ensayo SPT

E = m · g · h
m = masa de la maza
g = aceleración de la gravedad
h = altura de caída
Para un ensayo estándar, m = 63,5 kg; g = 9,81 m/s²; h = 0,76 m.

E = 473,43 J

Factor de corrección debido a la energía de impacto

Esta corrección se debe principalmente a pérdidas por rozamiento, que hacen que la energía teórica no se corresponde con la energía realmente liberada.

El valor corregido para N60 = Er · N / 60, siendo Er la relación de energías del equipo de ensayo y N el golpeo medido. El valor de Er depende del tipo de maquinaría y otros factores, debiéndose medir in situ y como valor teórico se puede adoptar un valor igual a 75 (e incluso inferior). N60 = 75 · N / 60
Obtenemos un valor de 1,25 para el factor de corrección por energía.

Perdidas debidas a la longitud del varillaje (λ)

Esta corrección se debe aplicar para profundidades inferiores a 10 m. Según la relación: 0,75 para profundidades inferiores a 4 m; 0,85 entre 4 y 6 m; 0,95 entre 6 y 10 m.

Efecto de la sobrecarga del terreno (Cn)

El factor de corrección se obtiene de la expresión:

Aplicación factores de corrección:

N = valor SPT (N30)

Ejemplo:
SPT realizado en un suelo= aluvial (SUCS GM), N30 = 18, profundidad 6,5 m. ρ = 21 kN/m³.
σ = 6,5 m · 21 kN/m³ = 136,5 kN/m²
Er/60 = 1,25
λ = 1
Cn = 0,847
N60 = 18 · 1,25 · 1 · 0,847 = 19

Ensayo de carga con placa.

A partir del ensayo de carga con placa (NLT 357/98), se puede establecer la categoría de un suelo y de ese modo conocer su usabilidad.

En nuestro ejemplo usaremos una placa circular rígida de Ø 300mm. El elemento de reacción es un camión de 20 T.

El ensayo se realiza con una serie de escalones de carga en tres ciclos. Los valores de presión dependen del tipo de uso al que se va a destinar el suelo, núcleo de terraplén, bases, relleno de tierras, … El primer ciclo es de carga, seguido por uno de descarga y a continuación se realiza el segundo ciclo de carga. En todos los ciclos, se miden los asientos en mm, con comparadores de precisión 1/100 mm.

En función del tipo de suelo, suele ser conveniente someterlo a una precarga de 0,01 Mpa (1kg/cm²) con objeto de obtener unos asientos mas reales al aplicar el primer ciclo de carga.

Con estos datos del ensayo, se pueden realizar los cálculos. El módulo de compresibilidad, se calcula mediante la fórmula:
E = 1,5 · r · ( ΔP / ΔS)
E = Módulo de compresibilidad (MPa)
ø = Diámetro de la placa de carga (cm)
r = radio (cm)
ΔP =Variación de carga (Kg/ cm²)
ΔS =Variación de asiento (mm)
En nuestro caso, los escalones escogidos para el cálculo de los módulos son 0,35 y 0,25 Mpa, con un S = 0,13 mm para el primer ciclo (Ev1) y 0,07 mm para el segundo ciclo.

Siendo:
Ev1 = 173,0 Mpa
Ev2 = 321,5 Mpa
Relación entre módulos (Ev2/Ev1) = 1,86

Módulo de reacción (Ks)

La norma establece que para el cálculo del módulo de reacción (Ks) hay que utilizar la placa de diámetro 762 mm y realizar una carga hasta conseguir un asiento de 1,25 mm. En este momento, se puede aplicar la fórmula:
Ks = ΔP / ΔS

En la práctica, el uso de la placa de 300 mm con una presión de 0,35 Mpa ofrece un valor estimado de Ks muy similar, por lo que en casos muy particulares y en función de la experiencia regional, se puede estimar Ks de esta manera.

Y en nuestro ejemplo, sería Ks = 6,5 kg/cm³ (65 kN/m³).

Módulo de Elasticidad (E)

Boussinesq estableció un método analítico aplicable a las placas circulares rígidas.

La fórmula será:

E = módulo de deformación (Mpa)
v = coeficiente de poisson
Ev = módulo de compresibilidad (Mpa)

Para nuestro ejemplo, asumiendo v=0,4 y con Ev = 321,5 Mpa obtenemos

E = 282 Mpa

Correlación empírica E y CBR

El módulo de deformación, se puede relacionar con el índice CBR mediante la expresión:

E = 10 * CBR

y en nuestro ejemplo, el valor del índice CBR sería = 28,2

Conclusiones

Del ensayo de carga con placa, obtenemos los módulos de compresibilidad (Ev), relación entre módulos, reacción (Ks), deformación (E) e índice CBR.

Con estos valores, en el caso de que estemos en el caso de dimensionamiento de firmes, se puede definir la categoría de la explanada, que en nuestro caso sería E3.

Micropilotes en Roca. Cimentaciones

Los micropilotes en roca, trabajan al igual que en suelos exclusivamente por el fuste, sin embargo, a efectos de cálculo solo se considera el fuste en el empotramiento en roca.

El tope estructural se puede calcular según el método indicado «Micropilotes en Suelos», sin embargo, a continuación se muestran otras maneras de calcular ese tope estructural de los micropilotes.

En el ejemplo que trataremos las características de los micropilotes serán:
Tubo TM80
Ø perforación (mm) = 165
Ø tubo armadura (mm) = 114,3
espesor pared armadura = 7 mm
límite elástico acero armadura = 5500 kg/cm²

Caso 1: se basa exclusivamente en el aporte de las armaduras despreciando la contribución del hormigón dada la escasa entidad del mismo. En este caso, la hipótesis de cálculo es la que considera unas condiciones mas favorables, por lo que es adecuado asumir un coeficiente de seguridad al tope estructural calculado de 1,5.

El límite elástico hay que minorarlo (coef. 1,5), por lo que será de 3666 kg/cm². Y el tope estructural vendrá dado por la expresión:
T.E. = límite elástico * sección tubo * π

La sección del tubo, será la sección total – la sección correspondiente al hormigón (cilindro vacío)

sección acero (m²) = * [(114,3/2)^2 – (114,3-14)/2)^2)] = 0,0024
T.E.= 0,0366 T/mm² * 2400 mm²
T.E. = 87,84 T / F.S.
T.E. = 58,56 T

Caso 2: según la «guía para el proyecto y ejecución de micropilotes en obras de carretera».

Siendo el tope estructural:
T.E. = 60,56 T

Caso 3: basado en las recomendaciones de la EHE-91. En este caso se tiene en cuenta tanto el acero como el hormigón, sin embargo se aplican unos coeficientes de minoración tanto al valor Fck del hormigón como al Fyk (límite elástico armadura).
Los valores de cálculo serían:
A = sección acero (m²) = 0,0024
B = sección hormigón (m²) = 0,0079
TE = (0,85•fck • B + fyk • A) / 2,16
cumpliéndose que A > 0,2 B
T.E. = 60,84 T

Se han utilizado tres métodos de cálculo diferentes, obteniendo unos valores muy similares.
Caso 1: 58,56 T
Caso 2: 60,56 T
Caso 3: 60,84 T

---

Supongamos ahora, que tenemos un encepado que transmitirá una carga axil mayorada de 100T. Redondeando y simplificando, podemos admitir que necesitaremos 2 micropilotes, soportando cada uno aproximadamente 50T.

En cualquier caso, el micropilote considerado cumple sobradamente (58,56T en el peor de los casos), por lo que el siguiente paso es calcular la longitud de empotramiento en roca necesaria.

Los micropilotes se empotrarán en un estrato calcáreo situado a 9 m de profundidad con una potencia estimada de centenares de metros según datos del estudio geotécnico.

La carga admisible, vendrá dada por la superficie de rozamiento entre micropilote – terreno y la resistencia unitaria por el fuste; aunque existen varias maneras de hacer los cálculos dependiendo de la información del estudio geotécnico.

En caso de no tener estudio geotécnico o de no estar completamente de acuerdo con la información y cálculos del mismo, se puede tirar de tablas, aunque en este caso siempre es importante la experiencia del técnico encargado de hacer los cálculos.

En una primera hipótesis, consideramos el sustrato rocoso como duro, admitiendo una resistencia unitaria por el fuste de entre 10-25 kg/cm² (según tablas) y aplicando un factor de seguridad de 1,5. Considerando el peor de los escenarios (10 kg/cm²), obtenemos una resistencia unitaria por fuste para los cálculos de 6,60 kg/cm².

La carga unitaria (ml) vendrá dada por la expresión: π * Ø perforación * ζuf

ζfc = π * 16,5 cm * 6,6 kg/cm² = 34,2 T / ml

Es decir, por cada ml de empotramiento en roca, tenemos 34,2T de resistencia; al necesitar 50T deberemos empotrar los micropilotes un mínimo de 2m en roca.

Otro método de cálculo es el indicado en la «guía para el proyecto y ejecución de micropilotes en obras de carretera», obteniéndose igualmente un valor similar.

Siendo la longitud de cada micropilote de 11 m (9m + 2m).

Empujes sobre un muro. Empuje activo

Uno de los apartados del estudio geotécnico, es el referido a los empujes en caso de haber sótanos, contención de tierras, …

En el siguiente ejemplo, se realiza un estudio geotécnico para la caracterización geotécnica de un terreno que se va a excavar y que para su contención se va a construir un muro en ménsula.

En este caso, contamos con un nivel freático y el trasdós del muro no es vertical, siendo el ancho de coronación del muro menor que la base. Los datos geométricos del muro no son de importancia ya que no se va a calcular ni dimensionar el muro.

Los datos de partida son:
ángulo de rozamiento terreno  φ = 25º
ángulo de rozamiento muro – terreno  δ = 15º (según CTE)
ángulo terreno coronación  β = 15º
peso específico suelo seco  γ = 23 kN/m³
peso específico suelo sumergido γ’= 13 kN/m³
peso específico agua γw = 10 kN/m³
ángulo trasdos – horizontal = 86,6º (por geometría)
altura del muro (desde la base de cimentación) H = 3,0 m
altura del nivel de agua desde coronación muro h = 1,6 m

Para calcular el coeficiente de empuje activo, se utilizan las fórmulas clásicas que se pueden consultar en cualquier bibliografía. En nuestro caso, estamos en el peor de los casos posibles a efectos de cálculo, trasdós no vertical, presencia de agua, …

Obteniendo:
coeficiente de empuje activo   Ea = 0,504
coeficiente de empuje activo horizontal  Eah = 0,478
coeficiente de empuje activo vertical    Eav= 0,159

Para calcular el empuje activo, y dado que tenemos nivel freático, se descompone este empuje en los siguientes:
– empuje debido al nivel de tierras por encima de la capa freática
– empuje debido a la carga equivalente del nivel superior sobre el nivel sumergido
– empuje debido al nivel de tierras sumergido
– empuje debido al nivel del agua en la zona sumergida

a) Empuje debido al nivel de tierras por encima de la capa freática

Siendo z la altura del nivel del terreno situado por encima del nivel de agua y y el peso específico del terreno seco.
El valor obtenido para el empuje = 14,84 kN/m
En cuanto a la presión del terreno:

Siendo P = 18,55 kN/m²
Y el punto de aplicación de este empuje se puede calcular mediante y=2z/3 = 1,07m

b) Empuje debido a la carga equivalente del nivel superior sobre el nivel sumergido

Siendo H la altura total de muro desde la base de cimentación.
El valor obtenido para el empuje = 25,97 kN/m
y la presion del terreno P = 18,55 kN/m²
En este caso, el punto de aplicación es y=z+(H-z)/2 = 2,30 m.

c) Empuje debido al nivel de tierras sumergido

Utilizando en este caso el valor del peso específco del suelo sumergido. El valor de E = 6,42 kN/m.
La presión P = 9,17 kN/m²
El punto de aplicación se calcula mediante y= z + 2(H-z)/3 = 2,53 m

d) Empuje debido al nivel del agua en la zona sumergida

E = 9,8 kN/m
La presión P = 14,0 kN/m²
El punto de aplicación se calcula mediante y= z + 2(H-z)/3 = 2,53 m

Con estos valores, se puede calcular el valor de la componente horizontal y vertical del empuje activo sobre el muro.

Obteniendo:
Empuje activo horizontal = 54,60 kN/m
Empuje activo vertical = 15,49 kN/m
Y el punto de aplicación de la resultante del empuje activo:

y = 2,05 m

Cimentaciones superficiales. Losas

Empleadas en aquellas zonas con baja capacidad portante o terrenos heterogéneos que podrían dar lugar a asientos diferenciales inadmisibles o cuando el uso de zapatas aisladas supone ocupar una superficie superior al 55% del total.

Sin embargo, en ocasiones las losas no resuelven el problema que plantean algunos suelos.

En este ejemplo, se calcularán los asientos estimados y la presión de trabajo para una losa  haciendo una estimación aproximada de las cargas y sobrecargas de la estructura.

Consideramos un suelo arcilloso (de 5m de potencia) en el que se han hecho varios ensayos de penetración estática CPT, obteniéndose una carga admisible del terreno de 45 kN/m² (0,45 kg/cm²).

La estructura a cimentar constará de:

– Cubierta
– Tres (3) plantas superiores
– Planta semi-sótano (losa + sobrecarga)
– Superficie en planta 12×20 m (240 m²)

Existen varios métodos para estimar de una manera rápida la carga que la estructura transmitirá al terreno. Aquí se explicarán dos, y dado que son estimaciones simples de un problema complejo, en los cálculos se suele prescindir de la carga que suponen las tierras excavadas (quedando del lado de la seguridad):

a) En este primer método, se estiman pesos y sobrecargas de uso fijos basados en la experiencia. En general se aplica un carga de 600 kg/m² para la cubierta, 800 kg/m² para las plantas superiores, y 2.200 kg/m² para la planta baja o semisótano que incluye la cimentación.

– cubierta: 1×600 kg/m² = 600 kg/m²
– plantas superiores: 3×800 kg/m² = 2.400 kg/m²
– losa + semisotano: 1×2.200 kg/m² = 2.200 kg/m²

Siendo en este caso la carga que transmitirá el edificio de 5.200 kg/m² = 5,2 T/m² = 52 kN/m².

Este sencillo método, tiene el inconveniente de ser demasiado conservador, sin embargo, siempre nos permite estar del lado de la seguridad.

b) El siguiente método que describiremos, es algo mas preciso, aunque tiene el inconveniente de tener que conocer datos estructurales y geométricos de la estructura.

Para el peso del forjado, se puede tomar un valor de 3 kN/m², tomándose un valor de corrección de 1,1 para la cubierta, 1,3 para las plantas superiores y 1,0 para la planta baja o semisotáno. Este valor de corrección servirá para estimar los cerramientos lineales de la estructura y compensar las cargas vivas y sobrecargas.

Igualmente, se debe conocer o al menos estimar el canto y dimensiones de la losa, para calcular el peso de la misma. El canto de la losa en nuestro ejemplo será de 0,60 m.

– cubierta; 300 kg/m² + 200 kg/m² (cp) + 100 kg/m² (sp) * 0,7 (fc) = 570 kg/m²
– plantas superiores: [300 kg/m² + 200 kg/m² (cp) + 200 kg/m² (sp) * 0,7 (fc) ]* 3 plantras = 1920 kg/m²
– semisotano + cimentación: (300 kg/m² + 0,6 m * 25 + 100 kg/m² (cp)) * 4 plantas = 1660 kg/m².
Los pesos totales serían (sup. 240m²):
– cubierta = 136.800 kg
– plantas superiores = 460.800 kg
– cimentación = 398.400 kg

Siendo el peso total = 996 T que equivale a 4,15 T/m² = 42 kN/m².

---

Con estos sencillos cálculos, obtenemos una estimación de la tensión de trabajo de la losa. Según el primer método la cimentación no es viable (52 kN/m² > 45 kN/m²), pero si estimamos las cargas transmitidas al terreno usando el segundo método, la cimentación a priori si podría llevarse a cabo (42 kN/m² < 45 kN/m²).

---

Una vez estimada si la presión admisible del terreno es suficiente para la losa, se calculan los asientos.

Igualmente existen varios métodos para calcular asientos en suelos, y la elección de uno u otro suele depender del tipo de ensayos realizados o del propio criterio del técnico.
En nuestro ejemplo, dado que tenemos realizados varios ensayos CPT, usaremos el método propuesto por Terzaghi-Buismann:

En el primer caso, para una carga de 52 kN/m², el asiento obtenido es de 21,67 cm.
En el segundo caso, la carga es de 42 kN/m², y el asiento obtenido de 17,5 cm.


(En caso de utilizar el método elástico, considerando 0,3 para el coeficiente de poisson y E = 26,5 kg/cm², se obtiene un asiento de 21,84 cm para el primer caso, y 17,64 cm para el segundo caso).

Las normas nos permiten un asiento máximo de 2″ (5cm), por lo que en ambos casos, independientemente de la estimación de la carga de la estructura, la cimentación mediante losa en el nivel de arcillas debe descartarse, teniendo que recurrir a otro tipo de cimentación que no sea superficial, o bien, modificar la estructura a construir para que las tensiones transmitidas al terreno no sean superiores a 10 kN/m² (0,1 kg/cm²).

Estabilidad de Taludes. Rotura por cuñas.

Se plantea la realización de un talud de 15 m de altura adoptando un ángulo de 45º. El macizo rocoso, está formado por una alternancia de calizas y margocalizas dispuestas en estratos centimétricos (15-50cm). Los parámetros geotécnicos, obtenidos a partir de una estación geomécanica realizada in situ han sido los siguientes: c = 40 kN/m², ángulo de rozamiento interno 20º.

El talud, tendrá una dirección N040ºE y un buzamiento al SE. Se han detectado y medido las siguientes familias de discontinuidad:

E = 165/34º; J1 = 355/60º; J2 = 063/82º

De la proyección estereográfica se deduce una posible rotura por cuñas a favor de E-J1 y otra a favor de E-J2.

Para calcular la estabilidad de la posible rotura, se sigue la metodología empleada por Hoek y Bray (1977) descrita en el Manual de Taludes (IGME).

En un primer lugar, se adopta el método rápido considerando que si el factor de seguridad para terreno seco y sin cohesión es mayor de 2,0, se puede afirmar que el talud será estable en las peores condiciones de presión intersticial.

(A y B se obtienen de los ábacos para rotura por cuñas correspondientes). Obteniéndose:
E-J1        FS = 3,60
E-J2        FS = 0,61

La primera cuña, por tanto será estable, en el caso de la segunda se debe recurrir a una metodología mas precisa, en la que se tendrá en cuenta todos los factores que intervienen en la estabilidad del talud (altura, presencia de agua, parámetros geotécnicos, buzamientos, …). En este segundo caso, se debe volver a recurrir a las proyecciones estereográficas para el cálculo de los ángulos entre planos.


Siendo:

X= 5,68; Y=2,45; A=1,47; B=5,47

obteniéndose un valor de FS = 2,487 y siendo por tanto estable.

En la actualidad existen muchos programas informáticos que simplifican estos cálculos, aunque sus resultados dependen de la experiencia y criterio del técnico que introduce los datos.

Existen aplicaciones sencillas, que calculan el FS a partir de los datos obtenidos en la proyección estereográfica:

Y los que a partir de los datos geoestructurales medidos en campo y con los parámetros geotécnicos obtenidos en la estación geomecánica, calculan el FS.